
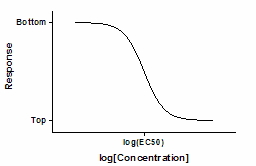
In order to choose the correct fit, it is important to understand the general shape of the model curves and compare them with the shape of the data points 2. The goal is also to find those parameter values that minimize the deviations between the measured and the expected values. In this case, the relationship between the measured values and the measurement variable is nonlinear. Nonlinear data are commonly modeled using logistic regression. However, in most cases, the relationship between measured values and measurement variables is nonlinear.įigure 1. The primary advantage of this method is that it is simple. The linear range of an assay can be determined using a minimum of three data points on the x-axis however, additional standard concentrations within the specified range should be added to improve the accuracy of the fit 1. SoftMax Pro will find the best straight line through the data (Figure 1). These are linear (y = A + Bx), semi-log (y = A + B * log 10(x)) and log-log (log 10(y) = A + B * log 10(x)). SoftMax Pro provides three linear regression curve-fitting methods. The slope of the line is B and A is the y intercept when x=0. It is represented by the equation y = A + Bx, where x (generally the concentration) is an independent variable and y (the response) is the dependent variable. The simplest method to analyze data is to use a linear regression curve fit. In addition, a protocol has been implemented with the sum of squared errors and the Akaike’s Information Criterion methods in order to evaluate different curve fit models to best represent the data. This technical note discusses the different linear and non-linear regression models available in SoftMax Pro 7. These ensure that the plotted curve is as close as possible to the curve that expresses the concentration versus response relationship by adjusting the curve fit parameters of the chosen model to best fit the data. SoftMax ® Pro 7 Software offers 21 different curve fit options, including the four parameter logistic (4P) and five parameter logistic (5P) nonlinear regression models.
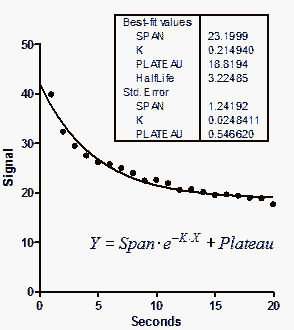
Therefore, the goal of curve fitting is to find the parameter values that most closely match the data, or in other words, the best mathematical equation that represents the empirical data.
The curve fit of choice should represent the most accurate relationship between two known variables: x and y.


 0 kommentar(er)
0 kommentar(er)
